Trading strategy time series

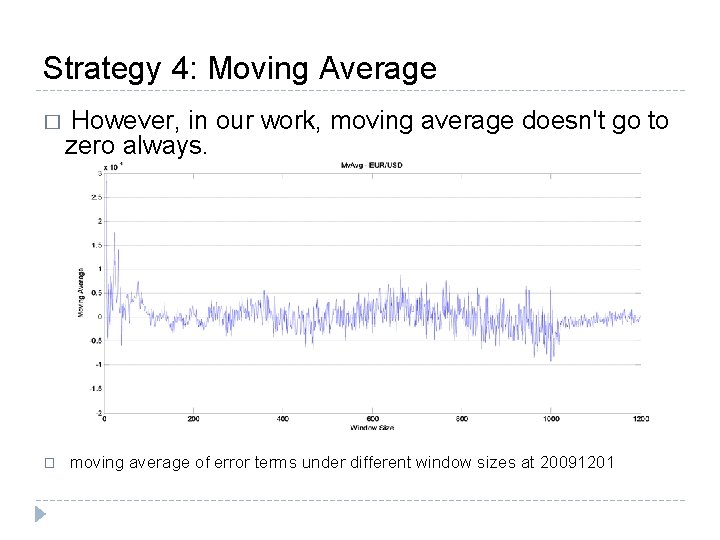
The inefficacy of the relevant time series momentum trading strategies rules out the possibility of speculations. However, the number of profitable momentum strategies is significantly higher for the diversified portfolios in longer run. The portfolios perform significantly better in outperforming the buy-only strategies as well.

The stable market, escalated demand and the resulting increment in valuation of green stocks make adoption of greener technologies a choice rather than a forced obligation. This offers a solution to the problem of Tragedy of Common. Presence of momentum profit would invite speculators leading to irrational exuberance, dwindling confidence and consequent fragility. Literature on green investment is relatively sparse with the threat of its vulnerability issues left largely unnoticed. Handle: RePEc:eme:sefpps:sef as.

Statistics Access and download statistics.

Corrections All material on this site has been provided by the respective publishers and authors. Louis Fed. Time series data typically contains a mix of various patterns that can be decomposed into several components, each representing an underlying pattern category. In particular, time series often consist of the systematic components trend, seasonality and cycles, and unsystematic noise. These components can be combined in an additive, linear model, in particular when fluctuations do not depend on the level of the series, or in a non-linear, multiplicative model.

The pandas library includes very flexible functionality to define various window types, including rolling, exponentially weighted and expanding windows. Autocorrelation also called serial correlation adapts the concept of correlation to the time series context: just as the correlation coefficient measures the strength of a linear relationship between two variables, the autocorrelation coefficient measures the extent of a linear relationship between time series values separated by a given lag.

The statistical properties, such as the mean, variance, or autocorrelation, of a stationary time series are independent of the period, that is, they don't change over time. Hence, stationarity implies that a time series does not have a trend or seasonal effects and that descriptive statistics, such as the mean or the standard deviation, when computed for different rolling windows, are constant or do not change much over time.

To satisfy the stationarity assumption of linear time series models, we need to transform the original time series, often in several steps. Common transformations include the application of the natural logarithm to convert an exponential growth pattern into a linear trend and stabilize the variance, or differencing. Unit roots pose a particular problem for determining the transformation that will render a time series stationary. In practice, time series of interest rates or asset prices are often not stationary, for example, because there does not exist a price level to which the series reverts.

The most prominent example of a non-stationary series is the random walk. The defining characteristic of a unit-root non-stationary series is long memory: since current values are the sum of past disturbances, large innovations persist for much longer than for a mean-reverting, stationary series. Identifying the correct transformation, and in particular, the appropriate number and lags for differencing is not always clear-cut. We present a few heuristics to guide the process. Statistical unit root tests are a common way to determine objectively whether additional differencing is necessary.

These are statistical hypothesis tests of stationarity that are designed to determine whether differencing is required.

Univariate time series models relate the value of the time series at the point in time of interest to a linear combination of lagged values of the series and possibly past disturbance terms. While exponential smoothing models are based on a description of the trend and seasonality in the data, ARIMA models aim to describe the autocorrelations in the data. ARIMA p, d, q models require stationarity and leverage two building blocks: - Autoregressive AR terms consisting of p-lagged values of the time series - Moving average MA terms that contain q-lagged disturbances.

An AR model of order p aims to capture the linear dependence between time series values at different lags. It closely resembles a multiple linear regression on lagged values of the outcome. An MA model of order q uses q past disturbances rather than lagged values of the time series in a regression-like model. Since we do not observe the white-noise disturbance values, MA q is not a regression model like the ones we have seen so far.

Autoregressive integrated moving-average ARIMA p, d, q models combine AR p and MA q processes to leverage the complementarity of these building blocks and simplify model development by using a more compact form and reducing the number of parameters, in turn reducing the risk of overfitting.

A particularly important area of application for univariate time series models is the prediction of volatility. The volatility of financial time series is usually not constant over time but changes, with bouts of volatility clustering together. The development of a volatility model for an asset-return series consists of four steps: 1.

Sensitivity of Trading Strategy

Specify a volatility model if serial correlation effects are significant, and jointly estimate the mean and volatility equations. Check the fitted model carefully and refine it if necessary. Multivariate time series models are designed to capture the dynamic of multiple time series simultaneously and leverage dependencies across these series for more reliable predictions. Univariate time-series models like the ARMA approach are limited to statistical relationships between a target variable and its lagged values or lagged disturbances and exogenous series in the ARMAX case.

In contrast, multivariate time-series models also allow for lagged values of other time series to affect the target. This effect applies to all series, resulting in complex interactions. In addition to potentially better forecasting, multivariate time series are also used to gain insights into cross-series dependencies. For example, in economics, multivariate time series are used to understand how policy changes to one variable, such as an interest rate, may affect other variables over different horizons.

The vector autoregressive VAR p model extends the AR p model to k series by creating a system of k equations where each contains p lagged values of all k series. Alternatively speaking, we invest in the asset in which the Machine Learning model gives the highest predicted probability that, a given asset will go up in value tomorrow. The model can be expanded to short selling and multi-asset purchasing and multi-periods. Pre-define a few intialisation objects and set the ticker symbols of the companies we want to download.

For this task I am not really interested in which companies I apply the strategy to. Once the data has been downloaded and stored into a new environment I clean the data up a little, put all the lists into a single data frame, compute the daily returns for each asset and create the up or down direction which will be what the classification model will try to predict. I split the time series data into a number of lists such that the analysis list contains observations in each list and has a corresponding assessment list which contains 1 observation.

In order to create the time series variables I use the tsfeatures package but there is also the feasts packages here. For this model I simply select a few functions of interest from the tsfeatures package. I wrote this code a little while ago and at the time I wrapped the model into a function. I think it would be more fun to exclusively stick to using just map functions instead of function SYMB. The function does the following for each asset in our data:. Next apply the functions character string to call the functions from the tsfeatures package, apply these functions to the in-sample analysis data which consists of observations each , such that, we obtain a single collapsed down observation that we can just bind together.